The crypto 2.0 business has been making robust progress up to now 12 months growing blockchain know-how, together with the formalization and in some instances realization of proof of stake designs like Slasher and DPOS, numerous varieties of scalable blockchain algorithms, blockchains utilizing “leader-free consensus” mechanisms derived from conventional Byzantine fault tolerance concept, in addition to financial elements like Schelling consensus schemes and secure currencies. All of those applied sciences treatment key deficiencies of the blockchain design with respect to centralized servers: scalability knocks down dimension limits and transaction prices, leader-free consensus reduces many types of exploitability, stronger PoS consensus algorithms scale back consensus prices and enhance safety, and Schelling consensus permits blockchains to be “conscious” of real-world knowledge. Nevertheless, there may be one piece of the puzzle that each one approaches up to now haven’t but managed to crack: privateness.
Forex, Dapps and Privateness
Bitcoin brings to its customers a reasonably distinctive set of tradeoffs with respect to monetary privateness. Though Bitcoin does a considerably higher job than any system that got here earlier than it at defending the bodily identities behind every of its accounts – higher than fiat and banking infrastructure as a result of it requires no identification registration, and higher than money as a result of it may be mixed with Tor to utterly cover bodily location, the presence of the Bitcoin blockchain signifies that the precise transactions made by the accounts are extra public than ever – neither the US authorities, nor China, nor the 13 12 months previous hacker down the road even want a lot as a warrant so as to decide precisely which account despatched how a lot BTC to which vacation spot at what specific time. Generally, these two forces pull Bitcoin in reverse instructions, and it’s not solely clear which one dominates.
With Ethereum, the scenario is analogous in concept, however in apply it’s reasonably totally different. Bitcoin is a blockchain supposed for foreign money, and foreign money is inherently a really fungible factor. There exist methods like merge avoidance which permit customers to basically faux to be 100 separate accounts, with their pockets managing the separation within the background. Coinjoin can be utilized to “combine” funds in a decentralized manner, and centralized mixers are possibility too particularly if one chains a lot of them collectively. Ethereum, however, is meant to retailer intermediate state of any form of processes or relationships, and sadly it’s the case that many processes or relationships which are considerably extra complicated than cash are inherently “account-based”, and enormous prices can be incurred by making an attempt to obfuscate one’s actions through a number of accounts. Therefore, Ethereum, because it stands as we speak, will in lots of instances inherit the transparency aspect of blockchain know-how rather more so than the privateness aspect (though these involved in utilizing Ethereum for foreign money can definitely construct higher-privacy money protocols inside subcurrencies).
Now, the query is, what if there are instances the place individuals actually need privateness, however a Diaspora-style self-hosting-based answer or a Zerocash-style zero-knowledge-proof technique is for no matter cause not possible – for instance, as a result of we wish to carry out calculations that contain aggregating a number of customers’ personal knowledge? Even when we remedy scalability and blockchain knowledge belongings, will the shortage of privateness inherent to blockchains imply that we merely have to return to trusting centralized servers? Or can we provide you with a protocol that gives the most effective of each worlds: a blockchain-like system which affords decentralized management not simply over the best to replace the state, however even over the best to entry the data in any respect?
Because it seems, such a system is properly throughout the realm of chance, and was even conceptualized by Nick Szabo in 1998 below the moniker of “God protocols” (although, as Nick Szabo identified, we should always not use that time period for the protocols that we’re about to explain right here as God is mostly assumed and even outlined to be Pareto-superior to the whole lot else and as we’ll quickly see these protocols are very removed from that); however now with the appearance of Bitcoin-style cryptoeconomic know-how the event of such a protocol could for the primary time truly be viable. What is that this protocol? To provide it a fairly technically correct however nonetheless comprehensible time period, we’ll name it a “secret sharing DAO”.
Fundamentals: Secret Sharing
To skip the enjoyable technical particulars and go straight to purposes, click on right here
Secret computation networks depend on two elementary primitives to retailer info in a decentralized manner. The primary is secret sharing. Secret sharing basically permits knowledge to be saved in a decentralized manner throughout N events such that any Ok events can work collectively to reconstruct the information, however Ok-1 events can not recuperate any info in any respect. N and Ok may be set to any values desired; all it takes is just a few easy parameter tweaks within the algorithm.
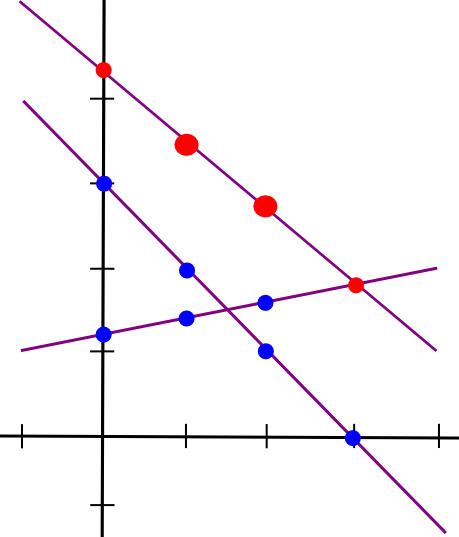
The only technique to mathematically describe secret sharing is as follows. We all know that two factors make a line:
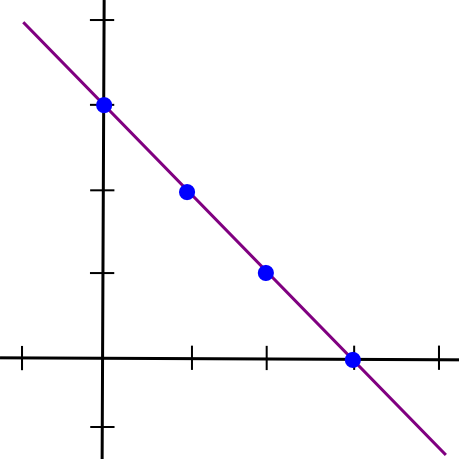
So, to implement 2-of-N secret sharing, we take our secret S, generate a random slope m, and create the road y = mx + S. We then give the N events the factors on the road (1, m + S), (2, 2m + S), (3, 3m + S), and so forth. Any two of them can reconstruct the road and recuperate the unique secret, however one individual can do nothing; for those who obtain the purpose (4, 12), that may very well be from the road y = 2x + 4, or y = -10x + 52, or y = 305445x – 1221768. To implement 3-of-N secret sharing, we simply make a parabola as a substitute, and provides individuals factors on the parabola:
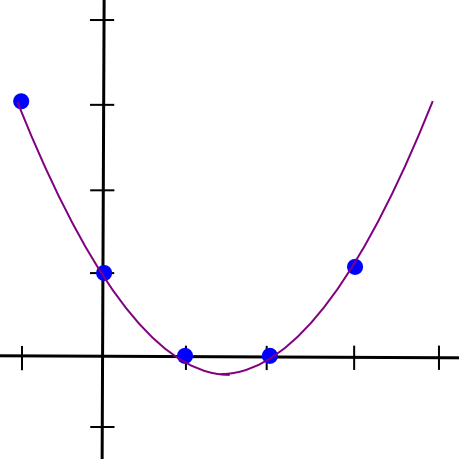
Parabolas have the property that any three factors on a parabola can be utilized to reconstruct the parabola (and nobody or two factors suffice), so basically the identical course of applies. And, extra usually, to implement Ok-of-N secret sharing, we use a level Ok-1 polynomial in the identical manner. There’s a set of algorithms for recovering the polynomial from a adequate set of factors in all such instances; they’re described in additional particulars in our earlier article on erasure coding.
That is how the key sharing DAO will retailer knowledge. As an alternative of each taking part node within the consensus storing a duplicate of the complete system state, each taking part node within the consensus will retailer a set of shares of the state – factors on polynomials, one level on a unique polynomial for every variable that makes up a part of the state.
Fundamentals: Computation
Now, how does the key sharing DAO do computation? For this, we use a set of algorithms known as safe multiparty computation (SMPC). The essential precept behind SMPC is that there exist methods to take knowledge which is break up amongst N events utilizing secret sharing, carry out computations on it in a decentralized manner, and find yourself with the consequence secret-shared between the events, all with out ever reconstituting any of the information on a single gadget.
SMPC with addition is straightforward. To see how, let’s return to the two-points-make-a-line instance, however now let’s have two strains:
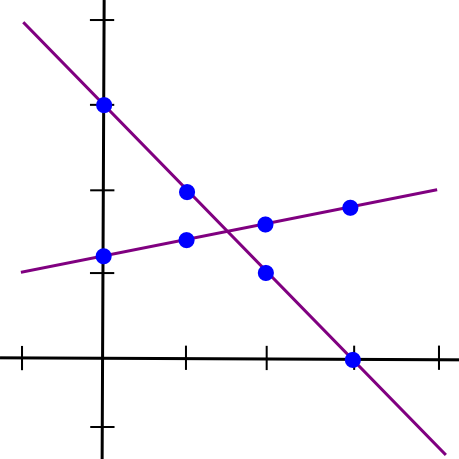
Suppose that the x=1 level of each strains A and B is saved by laptop P[1], the x=2 level is saved by laptop P[2], and so forth. Now, suppose that P[1] computes a brand new worth, C(1) = A(1) + B(1), and B computes C(2) = A(2) + B(2). Now, let’s draw a line by means of these two factors:
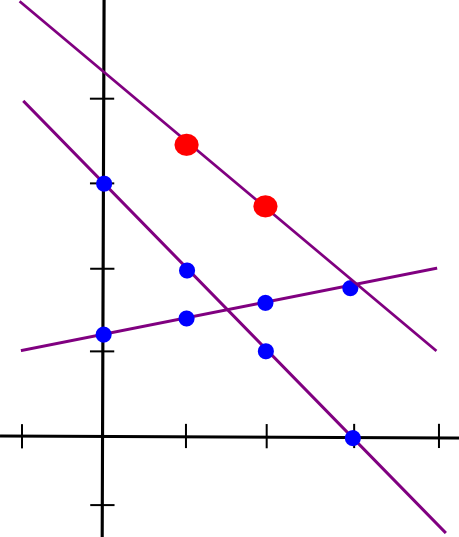
So we’ve got a brand new line, C, such that C = A + B at factors x=1 and x=2. Nevertheless, the fascinating factor is, this new line is definitely equal to A + B on each level:
Thus, we’ve got a rule: sums of secret shares (on the similar x coordinate) are secret shares of the sum. Utilizing this precept (which additionally applies to increased dimensions), we will convert secret shares of a and secret shares of b into secret shares of a+b, all with out ever reconstituting a and b themselves. Multiplication by a identified fixed worth works the identical manner: okay instances the ith secret share of a is the same as the ith secret share of a*okay.
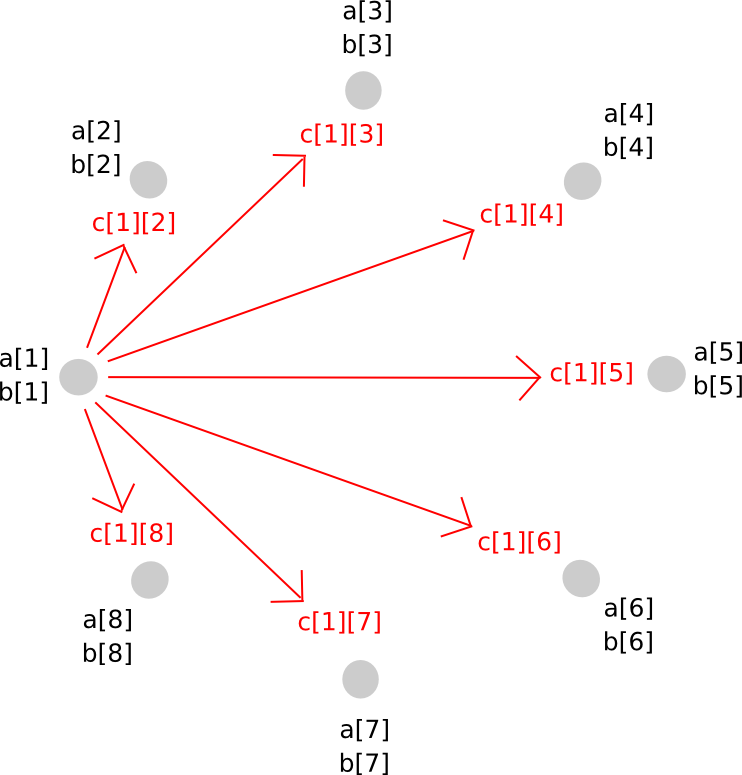
Multiplication of two secret shared values, sadly, is rather more concerned. The method will take a number of steps to clarify, and since it’s pretty sophisticated in any case it is value merely doing for arbitrary polynomials immediately. This is the magic. First, suppose that there exist values a and b, secret shared amongst events P[1] … P[n], the place a[i] represents the ith share of a (and similar for b[i] and b). We begin off like this:
Now, one possibility that you just would possibly consider is, if we will simply make a brand new polynomial c = a + b by having each occasion retailer c[i] = a[i] + b[i], cannot we do the identical for multiplication as properly? The reply is, surprisingly, sure, however with a significant issue: the brand new polynomial has a level twice as giant as the unique. For instance, if the unique polynomials have been y = x + 5 and y = 2x – 3, the product can be y = 2x^2 + 7x – 15. Therefore, if we do multiplication greater than as soon as, the polynomial would change into too large for the group of N to retailer.
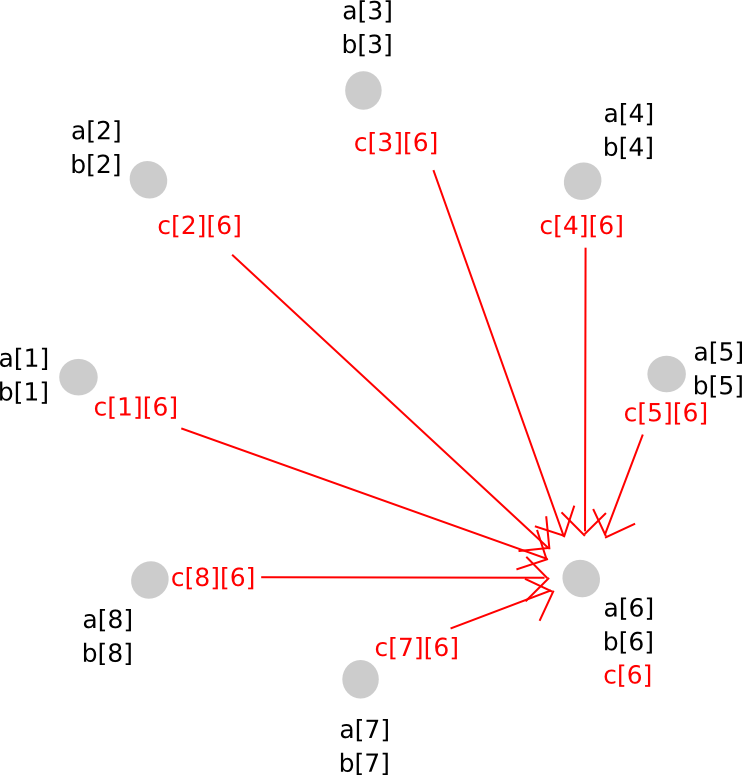
To keep away from this downside, we carry out a form of rebasing protocol the place we convert the shares of the bigger polynomial into shares of a polynomial of the unique diploma. The way in which it really works is as follows. First, occasion P[i] generates a brand new random polynomial, of the identical diploma as a and b, which evaluates to c[i] = a[i]*b[i] at zero, and distributes factors alongside that polynomial (ie. shares of c[i]) to all events.
Thus, P[j] now has c[i][j] for all i. Given this, P[j] calculates c[j], and so everybody has secret shares of c, on a polynomial with the identical diploma as a and b.
To do that, we used a intelligent trick of secret sharing: as a result of the key sharing math itself entails nothing greater than additions and multiplications by identified constants, the 2 layers of secret sharing are commutative: if we apply secret sharing layer A after which layer B, then we will take layer A off first and nonetheless be protected by layer B. This permits us to maneuver from a higher-degree polynomial to a decrease diploma polynomial however keep away from revealing the values within the center – as a substitute, the center step concerned each layers being utilized on the similar time.
With addition and multiplication over 0 and 1, we’ve got the flexibility to run arbitrary circuits inside the SMPC mechanism. We are able to outline:
- AND(a, b) = a * b
- OR(a, b) = a + b – a * b
- XOR(a, b) = a + b – 2 * a * b
- NOT(a) = 1 – a
Therefore, we will run no matter packages we would like, though with one key limitation: we will not do secret conditional branching. That’s, if we had a computation if (x == 5) <do A> else <do B> then the nodes would wish to know whether or not they’re computing department A or department B, so we would wish to disclose x halfway by means of.
There are two methods round this downside. First, we will use multiplication as a “poor man’s if” – exchange one thing like if (x == 5) <y = 7> with y = (x == 5) * 7 + (x != 5) * y, utilizing both circuits or intelligent protocols that implement equality checking by means of repeated multiplication (eg. if we’re in a finite area we will examine if a == b by utilizing Fermat’s little theorem on a-b). Second, as we are going to see, if we implement if statements contained in the EVM, and run the EVM inside SMPC, then we will resolve the issue, leaking solely the data of what number of steps the EVM took earlier than computation exited (and if we actually care, we will scale back the data leakage additional, eg. around the variety of steps to the closest energy of two, at some price to effectivity).
The key-sharing primarily based protocol described above is just one technique to do comparatively merely SMPC; there are different approaches, and to attain safety there may be additionally a necessity so as to add a verifiable secret sharing layer on prime, however that’s past the scope of this text – the above description is just meant to point out how a minimal implementation is feasible.
Constructing a Forex
Now that we’ve got a tough thought of how SMPC works, how would we use it to construct a decentralized foreign money engine? The overall manner {that a} blockchain is normally described on this weblog is as a system that maintains a state, S, accepts transactions, agrees on which transactions must be processed at a given time and computes a state transition operate APPLY(S, TX) -> S’ OR INVALID. Right here, we are going to say that all transactions are legitimate, and if a transaction TX is invalid then we merely have APPLY(S, TX) = S.
Now, because the blockchain isn’t clear, we’d count on the necessity for 2 sorts of transactions that customers can ship into the SMPC: get requests, asking for some particular details about an account within the present state, and replace requests, containing transactions to use onto the state. We’ll implement the rule that every account can solely ask for stability and nonce details about itself, and might withdraw solely from itself. We outline the 2 sorts of requests as follows:
SEND: [from_pubkey, from_id, to, value, nonce, sig] GET: [from_pubkey, from_id, sig]
The database is saved among the many N nodes within the following format:
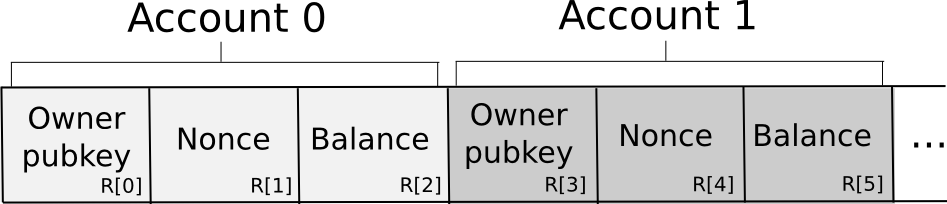
Primarily, the database is saved as a set of 3-tuples representing accounts, the place every 3-tuple shops the proudly owning pubkey, nonce and stability. To ship a request, a node constructs the transaction, splits it off into secret shares, generates a random request ID and attaches the ID and a small quantity of proof of labor to every share. The proof of labor is there as a result of some anti-spam mechanism is important, and since account balances are personal there is no such thing as a manner if the sending account has sufficient funds to pay a transaction charge. The nodes then independently confirm the shares of the signature towards the share of the general public key equipped within the transaction (there are signature algorithms that will let you do this type of per-share verification; Schnorr signatures are one main class). If a given node sees an invalid share (because of proof of labor or the signature), it rejects it; in any other case, it accepts it.
Transactions which are accepted will not be processed instantly, very like in a blockchain structure; at first, they’re stored in a reminiscence pool. On the finish of each 12 seconds, we use some consensus algorithm – it may very well be one thing easy, like a random node from the N deciding as a dictator, or a sophisticated neo-BFT algorithm like that utilized by Pebble – to agree on which set of request IDs to course of and wherein order (for simplicity, easy alphabetical order will in all probability suffice).
Now, to fufill a GET request, the SMPC will compute and reconstitute the output of the next computation:
owner_pubkey = R[0] * (from_id == 0) + R[3] * (from_id == 1) + ... + R[3*n] * (from_id == n) legitimate = (owner_pubkey == from_pubkey) output = legitimate * (R[2] * (from_id == 0) + R[5] * (from_id == 1) + ... + R[3n + 2] * (from_id == n))
So what does this components do? It consists of three phases. First, we extract the proprietor pubkey of the account that the request is making an attempt to get the stability of. As a result of the computation is completed inside an SMPC, and so no node truly is aware of what database index to entry, we do that by merely taking all of the database indices, multiplying the irrelevant ones by zero and taking the sum. Then, we examine if the request is making an attempt to get knowledge from an account which is definitely owns (do not forget that we checked the validity of from_pubkey towards the signature in step one, so right here we simply must examine the account ID towards the from_pubkey). Lastly, we use the identical database getting primitive to get the stability, and multiply the stability by the validity to get the consequence (ie. invalid requests return a stability of 0, legitimate ones return the precise stability).
Now, let’s take a look at the execution of a SEND. First, we compute the validity predicate, consisting of checking that (1) the general public key of the focused account is appropriate, (2) the nonce is appropriate, and (3) the account has sufficient funds to ship. Observe that to do that we as soon as once more want to make use of the “multiply by an equality examine and add” protocol, however for brevity we are going to abbreviate R[0] * (x == 0) + R[3] * (x == 1) + … with R[x * 3].
legitimate = (R[from_id * 3] == from_pubkey) * (R[from_id * 3 + 1] == nonce) * (R[from_id * 3 + 2] >= worth)
We then do:
R[from_id * 3 + 2] -= worth * legitimate R[from_id * 3 + 1] += legitimate R[to * 3 + 2] += worth * legitimate
For updating the database, R[x * 3] += y expands to the set of directions R[0] += y * (x == 0), R[3] += y * (x == 1) …. Observe that each one of those may be parallelized. Additionally, be aware that to implement stability checking we used the >= operator. That is as soon as once more trivial utilizing boolean logic gates, however even when we use a finite area for effectivity there do exist some intelligent methods for performing the examine utilizing nothing however additions and multiplications.
In the entire above we noticed two elementary limitations in effectivity within the SMPC structure. First, studying and writing to a database has an O(n) price as you just about should learn and write each cell. Doing something much less would imply exposing to particular person nodes which subset of the database a learn or write was from, opening up the opportunity of statistical reminiscence leaks. Second, each multiplication requires a community message, so the elemental bottleneck right here isn’t computation or reminiscence however latency. Due to this, we will already see that secret sharing networks are sadly not God protocols; they’ll do enterprise logic simply nice, however they are going to by no means have the ability to do something extra sophisticated – even crypto verifications, except for a choose few crypto verifications particularly tailor-made to the platform, are in lots of instances too costly.
From Forex to EVM
Now, the subsequent downside is, how can we go from this straightforward toy foreign money to a generic EVM processor? Properly, allow us to study the code for the digital machine inside a single transaction surroundings. A simplified model of the operate appears to be like roughly as follows:
def run_evm(block, tx, msg, code): laptop = 0 fuel = msg.fuel stack = [] stack_size = 0 exit = 0 whereas 1: op = code[pc] fuel -= 1 if fuel < 0 or stack_size < get_stack_req(op): exit = 1 if op == ADD: x = stack[stack_size] y = stack[stack_size - 1] stack[stack_size - 1] = x + y stack_size -= 1 if op == SUB: x = stack[stack_size] y = stack[stack_size - 1] stack[stack_size - 1] = x - y stack_size -= 1 ... if op == JUMP: laptop = stack[stack_size] stack_size -= 1 ...
The variables concerned are:
- The code
- The stack
- The reminiscence
- The account state
- This system counter
Therefore, we will merely retailer these as data, and for each computational step run a operate just like the next:
op = code[pc] * alive + 256 * (1 - alive) fuel -= 1 stack_p1[0] = 0 stack_p0[0] = 0 stack_n1[0] = stack[stack_size] + stack[stack_size - 1] stack_sz[0] = stack_size - 1 new_pc[0] = laptop + 1 stack_p1[1] = 0 stack_p0[1] = 0 stack_n1[1] = stack[stack_size] - stack[stack_size - 1] stack_sz[1] = stack_size - 1 new_pc[1] = laptop + 1 ... stack_p1[86] = 0 stack_p0[86] = 0 stack_n1[86] = stack[stack_size - 1] stack_sz[86] = stack_size - 1 new_pc[86] = stack[stack_size] ... stack_p1[256] = 0 stack_p0[256] = 0 stack_n1[256] = 0 stack_sz[256] = 0 new_pc[256] = 0 laptop = new_pc[op] stack[stack_size + 1] = stack_p1[op] stack[stack_size] = stack_p0[op] stack[stack_size - 1] = stack_n1[op] stack_size = stack_sz[op] laptop = new_pc[op] alive *= (fuel < 0) * (stack_size < 0)
Primarily, we compute the results of each single opcode in parallel, after which decide the proper one to replace the state. The alive variable begins off at 1, and if the alive variable at any level switches to zero, then all operations from that time merely do nothing. This appears horrendously inefficient, and it’s, however keep in mind: the bottleneck isn’t computation time however latency. The whole lot above may be parallelized. In truth, the astute reader could even discover that the complete strategy of working each opcode in parallel has solely O(n) complexity within the variety of opcodes (notably for those who pre-grab the highest few gadgets of the stack into specified variables for enter in addition to output, which we didn’t do for brevity), so it’s not even probably the most computationally intensive half (if there are extra accounts or storage slots than opcodes, which appears probably, the database updates are). On the finish of each N steps (or for even much less info leakage each energy of two of steps) we reconstitute the alive variable and if we see that alive = 0 then we halt.
In an EVM with many individuals, the database will probably be the biggest overhead. To mitigate this downside, there are probably intelligent info leakage tradeoffs that may be made. For instance, we already know that more often than not code is learn from sequential database indices. Therefore, one method is likely to be to retailer the code as a sequence of enormous numbers, every giant quantity encoding many opcodes, after which use bit decomposition protocols to learn off particular person opcodes from a quantity as soon as we load it. There are additionally probably some ways to make the digital machine essentially rather more environment friendly; the above is supposed, as soon as once more, as a proof of idea to point out how a secret sharing DAO is essentially doable, not something near an optimum implementation. Moreover, we will look into architectures just like those utilized in scalability 2.0 methods to extremely compartmentalize the state to additional enhance effectivity.
Updating the N
The SMPC mechanism described above assumes an present N events concerned, and goals to be safe towards any minority of them (or in some designs at the very least any minority lower than 1/4 or 1/3) colluding. Nevertheless, blockchain protocols must theoretically final eternally, and so stagnant financial units don’t work; reasonably, we have to choose the consensus individuals utilizing some mechanism like proof of stake. To do that, an instance protocol would work as follows:
- The key sharing DAO’s time is split into “epochs”, every maybe someplace between an hour and per week lengthy.
- Throughout the first epoch, the individuals are set to be the highest N individuals through the genesis sale.
- On the finish of an epoch, anybody has the flexibility to enroll to be one of many individuals within the subsequent spherical by placing down a deposit. N individuals are randomly chosen, and revealed.
- A “decentralized handoff protocol” is carried out, the place the N individuals concurrently break up their shares among the many new N, and every of the brand new N reconstitutes their share from the items that they obtained – basically, the very same protocol as was used for multiplication. Observe that this protocol can be used to extend or lower the variety of individuals.
All the above handles decentralization assuming trustworthy individuals; however in a cryptocurrency protocol we additionally want incentives. To perform that, we use a set of primitives known as verifiable secret sharing, that enable us to find out whether or not a given node was performing actually all through the key sharing course of. Primarily, this course of works by doing the key sharing math in parallel on two totally different ranges: utilizing integers, and utilizing elliptic curve factors (different constructions additionally exist, however as a result of cryptocurrency customers are most conversant in the secp256k1 elliptic curve we’ll use that). Elliptic curve factors are handy as a result of they’ve a commutative and associative addition operator – in essence, they’re magic objects which may be added and subtracted very like numbers can. You’ll be able to convert a quantity into a degree, however not a degree right into a quantity, and we’ve got the property that number_to_point(A + B) = number_to_point(A) + number_to_point(B). By doing the key sharing math on the quantity stage and the elliptic curve level stage on the similar time, and publicizing the elliptic curve factors, it turns into doable to confirm malfeasance. For effectivity, we will in all probability use a Schellingcoin-style protocol to permit nodes to punish different nodes which are malfeasant.
Functions
So, what do we’ve got? If the blockchain is a decentralized laptop, a secret sharing DAO is a decentralized laptop with privateness. The key sharing DAO pays dearly for this further property: a community message is required per multiplication and per database entry. Because of this, fuel prices are more likely to be a lot increased than Ethereum correct, limiting the computation to solely comparatively easy enterprise logic, and barring the usage of most sorts of cryptographic calculations. Scalability know-how could also be used to partially offset this weak spot, however in the end there’s a restrict to how far you will get. Therefore, this know-how will in all probability not be used for each use case; as a substitute, it should function extra like a special-purpose kernel that can solely be employed for particular sorts of decentralized purposes. Some examples embrace:
- Medical data – holding the information on a non-public decentralized platform can probably open the door for an easy-to-use and safe well being info system that retains sufferers answerable for their knowledge. Notably, be aware that proprietary analysis algorithms may run inside the key sharing DAO, permitting medical analysis as a service primarily based on knowledge from separate medical checkup corporations with out working the chance that they are going to deliberately or unintentionally expose your personal particulars to insurers, advertisers or different corporations.
- Non-public key escrow – a decentralized M-of-N various to centralized password restoration; may very well be used for monetary or non-financial purposes
- Multisig for something – even programs that don’t natively help arbitrary entry insurance policies, and even M-of-N multisignature entry, now will, since so long as they help cryptography you may stick the personal key inside a secret sharing DAO.
- Repute programs – what if status scores have been saved inside a secret sharing DAO so you might privately assign status to different customers, and have your task depend in direction of the entire status of that person, with out anybody with the ability to see your particular person assignments?
- Non-public monetary programs – secret sharing DAOs may present another path to Zerocash-style totally nameless foreign money, besides that right here the performance may very well be rather more simply prolonged to decentralized alternate and extra complicated sensible contracts. Enterprise customers could wish to leverage among the advantages of working their firm on prime of crypto with out essentially exposing each single one in every of their inside enterprise processes to most of the people.
- Matchmaking algorithms – discover employers, workers, relationship companions, drivers in your subsequent journey on Decentralized Uber, and so forth, however doing the matchmaking algorithm computations inside SMPC in order that nobody sees any details about you except the algorithm determines that you’re a excellent match.
Primarily, one can consider SMPC as providing a set of instruments roughly just like that which it has been theorized can be provided by cryptographically safe code obfuscation, besides with one key distinction: it truly works on human-practical time scales.
Additional Penalties
Other than the purposes above, what else will secret sharing DAOs carry? Notably, is there something to fret about? Because it seems, similar to with blockchains themselves, there are just a few considerations. The primary, and most blatant, problem is that secret sharing DAOs will considerably enhance the scope of purposes that may be carried out in a totally personal style. Many advocates of blockchain know-how typically base a big a part of their argument on the important thing level that whereas blockchain-based currencies supply an unprecedented quantity of anonymity within the sense of not linking addresses to particular person identities, they’re on the similar time probably the most public type of foreign money on this planet as a result of each transaction is positioned on a shared ledger. Right here, nonetheless, the primary half stays, however the second half disappears utterly. What we’ve got left is actually whole anonymity.
If it seems to be the case that this stage of anonymity permits for a a lot increased diploma of legal exercise, and the general public isn’t proud of the tradeoff that the know-how brings, then we will predict that governments and different establishments generally, even perhaps alongside volunteer vigilante hackers, will strive their finest to take these programs down, and maybe they might even be justified. Fortuitously for these attackers, nonetheless, secret sharing DAOs do have an inevitable backdoor: the 51% assault. If 51% of the maintainers of a secret sharing DAO at some specific time determine to collude, then they’ll uncover any of the information that’s below their supervision. Moreover, this energy has no statute of limitations: if a set of entities who fashioned over half of the sustaining set of a secret sharing DAO in some unspecified time in the future a few years in the past collude, then even then the group would have the ability to unearth the data from that cut-off date. In brief, if society is overwhelmingly against one thing being achieved inside a secret sharing DAO, there can be loads of alternative for the operators to collude to cease or reveal what is going on on.
A second, and subtler, problem is that the idea of secret sharing DAOs drives a stake by means of a cherished reality of cryptoeconomics: that personal keys will not be securely tradeable. Many protocols explicitly, or implicitly, depend on this concept, together with non-outsourceable proof of labor puzzles, Vlad Zamfir and Pavel Kravchenko’s proof of custody, financial protocols that use personal keys as identities, any form of financial standing that goals to be untradeable, and so forth. On-line voting programs typically have the requirement that it must be not possible to show that you just voted with a specific key, in order to stop vote promoting; with secret sharing DAOs, the issue is that now you truly can promote your vote, reasonably merely: by placing your personal key right into a contract inside a secret sharing DAO, and renting out entry.
The results of this potential to promote personal keys are fairly far reaching – in truth, they go as far as to virtually threaten the safety of the strongest obtainable system underlying blockchain safety: proof of stake. The potential concern is that this: proof of stake derives its safety from the truth that customers have safety deposits on the blockchain, and these deposits can probably be taken away if the person misacts in some style (double-voting, voting for a fork, not voting in any respect, and so forth). Right here, personal keys change into tradeable, and so safety deposits change into tradeable as properly. We should ask the query: does this compromise proof of stake?
Fortuitously, the reply is not any. To start with, there are robust lemon-theoretic arguments for why nobody would truly need to promote their deposit. You probably have a deposit of $10, to you that is value $10 minus the tiny likelihood that you’re going to get hacked. However for those who attempt to promote that deposit to another person, they are going to have a deposit which is value $10, except you determine to make use of your personal key to double-vote and thus destroy the deposit. Therefore, from their viewpoint, there’s a fixed overhanging danger that you’ll act to take their deposit away, and also you personally don’t have any incentive not to try this. The actual fact that you’re making an attempt to unload your deposit ought to make them suspicious. Therefore, from their viewpoint, your deposit would possibly solely be value, say, $8. You haven’t any cause to sacrifice $10 for $8, in order a rational actor you’ll hold the deposit to your self.
Second, if the personal key was within the secret sharing DAO proper from the beginning, then by transferring entry to the important thing you’ll personally lose entry to it, so you’ll truly switch the authority and the legal responsibility on the similar time – from an financial standpoint, the impact on the system can be precisely the identical as if one of many deposit holders merely had a change of persona in some unspecified time in the future through the course of. In truth, secret sharing DAOs could even enhance proof of stake, by offering a safer platform for customers to take part in decentralized stake swimming pools even in protocols like Tendermint, which don’t natively help such performance.
There are additionally different the explanation why the theoretical assaults that secret sharing DAOs make doable could in truth fail in apply. To take one instance, think about the case of non-outsourceable puzzles, computational issues which attempt to show possession of a non-public key and a chunk of information on the similar time. One form of implementation of a non-outsourceable puzzle, utilized by Permacoin, entails a computation which must “bounce” forwards and backwards between the important thing and the information a whole bunch of hundreds of instances. That is simple to do when you’ve got the 2 items of information on the identical piece of {hardware}, however turns into prohibitively sluggish if the 2 are separated by a community connection – and over a secret sharing DAO it will be almost not possible because of the inefficiencies. Because of this, one doable conclusion of all that is that secret sharing DAOs will result in the standardization of a signature scheme which requires a number of hundred hundreds of thousands of rounds of computation – ideally with tons and plenty of serial multiplication – to compute, at which level each laptop, telephone or internet-of-things microchip would have a built-in ASIC to do it trivially, secret sharing DAOs can be left within the mud, and we’d all transfer on with our lives.
How Far Away?
So what’s left earlier than secret sharing DAO know-how can go mainstream? In brief, fairly a bit, however not an excessive amount of. At first, there may be definitely a average quantity of technical engineering concerned, at the very least on the protocol stage. Somebody must formalize an SMPC implementation, along with how it will be mixed with an EVM implementation, in all probability with many restrictions for effectivity (eg. hash features inside SMPC are very costly, so Merkle tree storage could disappear in favor of each contract having a finite variety of storage slots), a punishment, incentive and consensus framework and a hypercube-style scalability framework, after which launch the protocol specification. From that time, it is just a few months of improvement in Python (Python must be nice, as by far the first bottleneck can be community latency, not computation), and we’ll have a working proof of idea.
Secret sharing and SMPC know-how has been on the market for a few years, and tutorial cryptographers have been speaking about tips on how to construct privacy-preserving purposes utilizing M-of-N-based primitives and associated applied sciences resembling personal info retrieval for over a decade. The important thing contribution made by Bitcoin, nonetheless, is the concept that M-of-N frameworks generally may be rather more simply bootstrapped if we add in an financial layer. A secret sharing DAO with a foreign money in-built would offer incentives for people to take part in sustaining the community, and would bootstrap it till the purpose the place it may very well be totally self-sustaining on inside purposes. Thus, altogether, this know-how is sort of doable, and never almost so distant; it’s only a matter of time till somebody does it.

