Gentle Shoppers and Proof of Stake

Particular due to Vlad Zamfir and Jae Kwon for lots of the concepts described on this put up

Other than the first debate round weak subjectivity, one of many vital secondary arguments raised in opposition to proof of stake is the difficulty that proof of stake algorithms are a lot more durable to make light-client pleasant. Whereas proof of labor algorithms contain the manufacturing of block headers which may be shortly verified, permitting a comparatively small chain of headers to behave as an implicit proof that the community considers a selected historical past to be legitimate, proof of stake is more durable to suit into such a mannequin. As a result of the validity of a block in proof of stake depends on stakeholder signatures, the validity will depend on the possession distribution of the foreign money within the explicit block that was signed, and so it appears, at the very least at first look, that as a way to acquire any assurances in any respect in regards to the validity of a block, the whole block have to be verified.

Given the sheer significance of sunshine shopper protocols, significantly in mild of the current company curiosity in “web of issues” functions (which should usually essentially run on very weak and low-power {hardware}), mild shopper friendliness is a vital characteristic for a consensus algorithm to have, and so an efficient proof of stake system should deal with it.

Gentle purchasers in Proof of Work

Generally, the core motivation behind the “mild shopper” idea is as follows. By themselves, blockchain protocols, with the requirement that each node should course of each transaction as a way to guarantee safety, are costly, and as soon as a protocol will get sufficiently in style the blockchain turns into so huge that many customers change into not even capable of bear that price. The Bitcoin blockchain is at present 27 GB in measurement, and so only a few customers are keen to proceed to run “full nodes” that course of each transaction. On smartphones, and particularly on embedded {hardware}, operating a full node is outright unimaginable.

Therefore, there must be a way through which a consumer with far much less computing energy to nonetheless get a safe assurance about numerous particulars of the blockchain state – what’s the steadiness/state of a selected account, did a selected transaction course of, did a selected occasion occur, and so on. Ideally, it must be doable for a light-weight shopper to do that in logarithmic time – that’s, squaring the variety of transactions (eg. going from 1000 tx/day to 1000000 tx/day) ought to solely double a light-weight shopper’s price. Luckily, because it seems, it’s fairly doable to design a cryptocurrency protocol that may be securely evaluated by mild purchasers at this stage of effectivity.

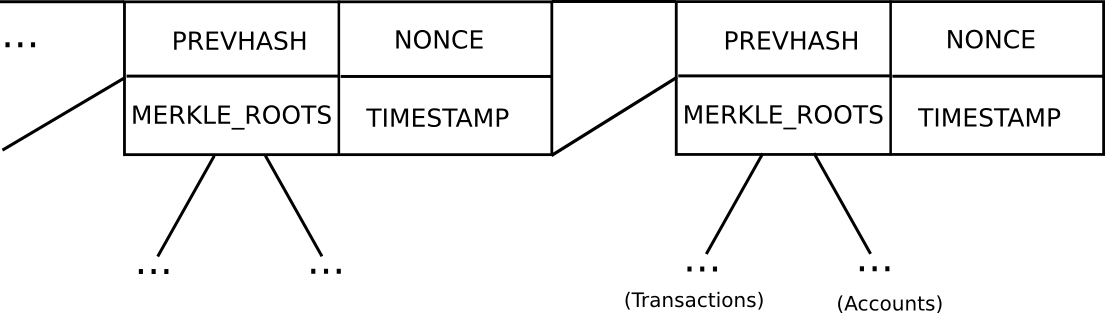
Fundamental block header mannequin in Ethereum (notice that Ethereum has a Merkle tree for transactions and accounts in every block, permitting mild purchasers to simply entry extra information)

In Bitcoin, mild shopper safety works as follows. As a substitute of establishing a block as a monolithic object containing all the transactions instantly, a Bitcoin block is break up up into two components. First, there’s a small piece of information known as the block header, containing three key items of information:

• The hash of the earlier block header
• The Merkle root of the transaction tree (see beneath)
• The proof of labor nonce

Further information just like the timestamp can also be included within the block header, however this isn’t related right here. Second, there’s the transaction tree. Transactions in a Bitcoin block are saved in an information construction known as a Merkle tree. The nodes on the underside stage of the tree are the transactions, after which going up from there each node is the hash of the 2 nodes beneath it. For instance, if the underside stage had sixteen transactions, then the following stage would have eight nodes: hash(tx[1] + tx[2]), hash(tx[3] + tx[4]), and so on. The extent above that might have 4 nodes (eg. the primary node is the same as hash(hash(tx[1] + tx[2]) + hash(tx[3] + tx[4]))), the extent above has two nodes, after which the extent on the high has one node, the Merkle root of the whole tree.

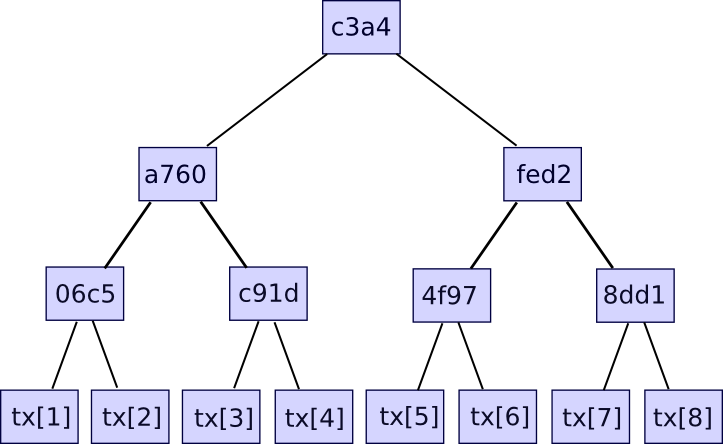
The Merkle root may be regarded as a hash of all of the transactions collectively, and has the identical properties that you’d count on out of a hash – in the event you change even one bit in a single transaction, the Merkle root will find yourself utterly totally different, and there’s no strategy to provide you with two totally different units of transactions which have the identical Merkle root. The explanation why this extra sophisticated tree building must be used is that it really permits you to provide you with a compact proof that one explicit transaction was included in a selected block. How? Primarily, simply present the department of the tree taking place to the transaction:

The verifier will confirm solely the hashes taking place alongside the department, and thereby be assured that the given transaction is legitimately a member of the tree that produced a selected Merkle root. If an attacker tries to vary any hash wherever taking place the department, the hashes will not match and the proof shall be invalid. The dimensions of every proof is the same as the depth of the tree – ie. logarithmic within the variety of transactions. In case your block comprises 2²⁰ (ie. ~1 million) transactions, then the Merkle tree may have solely 20 ranges, and so the verifier will solely have to compute 20 hashes as a way to confirm a proof. In case your block comprises 2³⁰ (ie. ~1 billion) transactions, then the Merkle tree may have 30 ranges, and so a light-weight shopper will be capable of confirm a transaction with simply 30 hashes.

Ethereum extends this primary mechanism with a two further Merkle timber in every block header, permitting nodes to show not simply {that a} explicit transaction occurred, but in addition {that a} explicit account has a selected steadiness and state, {that a} explicit occasion occurred, and even {that a} explicit account does not exist.

Verifying the Roots

Now, this transaction verification course of all assumes one factor: that the Merkle root is trusted. If somebody proves to you {that a} transaction is a part of a Merkle tree that has some root, that by itself means nothing; membership in a Merkle tree solely proves {that a} transaction is legitimate if the Merkle root is itself recognized to be legitimate. Therefore, the opposite vital a part of a light-weight shopper protocol is determining precisely how one can validate the Merkle roots – or, extra typically, how one can validate the block headers.

Initially, allow us to decide precisely what we imply by “validating block headers”. Gentle purchasers usually are not able to absolutely validating a block by themselves; protocols exist for doing validation collaboratively, however this mechanism is pricey, and so as a way to stop attackers from losing everybody’s time by throwing round invalid blocks we’d like a approach of first shortly figuring out whether or not or not a selected block header is most likely legitimate. By “most likely legitimate” what we imply is that this: if an attacker offers us a block that’s decided to be most likely legitimate, however shouldn’t be really legitimate, then the attacker must pay a excessive price for doing so. Even when the attacker succeeds in briefly fooling a light-weight shopper or losing its time, the attacker ought to nonetheless undergo greater than the victims of the assault. That is the usual that we are going to apply to proof of labor, and proof of stake, equally.

In proof of labor, the method is easy. The core concept behind proof of labor is that there exists a mathematical operate which a block header should fulfill as a way to be legitimate, and it’s computationally very intensive to provide such a legitimate header. If a light-weight shopper was offline for some time period, after which comes again on-line, then it would search for the longest chain of legitimate block headers, and assume that that chain is the respectable blockchain. The price of spoofing this mechanism, offering a series of block headers that’s probably-valid-but-not-actually-valid, may be very excessive; actually, it’s virtually precisely the identical as the price of launching a 51% assault on the community.

In Bitcoin, this proof of labor situation is easy: sha256(block_header) < 2**187 (in apply the “goal” worth modifications, however as soon as once more we are able to dispense of this in our simplified evaluation). So as to fulfill this situation, miners should repeatedly strive totally different nonce values till they arrive upon one such that the proof of labor situation for the block header is glad; on common, this consumes about 2⁶⁹ computational effort per block. The elegant characteristic of Bitcoin-style proof of labor is that each block header may be verified by itself, with out counting on any exterior info in any respect. Because of this the method of validating the block headers can actually be performed in fixed time – obtain 80 bytes and run a hash of it – even higher than the logarithmic sure that we have now established for ourselves. In proof of stake, sadly we shouldn’t have such a pleasant mechanism.

Gentle Shoppers in Proof of Stake

If we need to have an efficient mild shopper for proof of stake, ideally we want to obtain the very same complexity-theoretic properties as proof of labor, though essentially differently. As soon as a block header is trusted, the method for accessing any information from the header is identical, so we all know that it’ll take a logarithmic period of time as a way to do. Nonetheless, we would like the method of validating the block headers themselves to be logarithmic as effectively.

To begin off, allow us to describe an older model of Slasher, which was not significantly designed to be explicitly light-client pleasant:

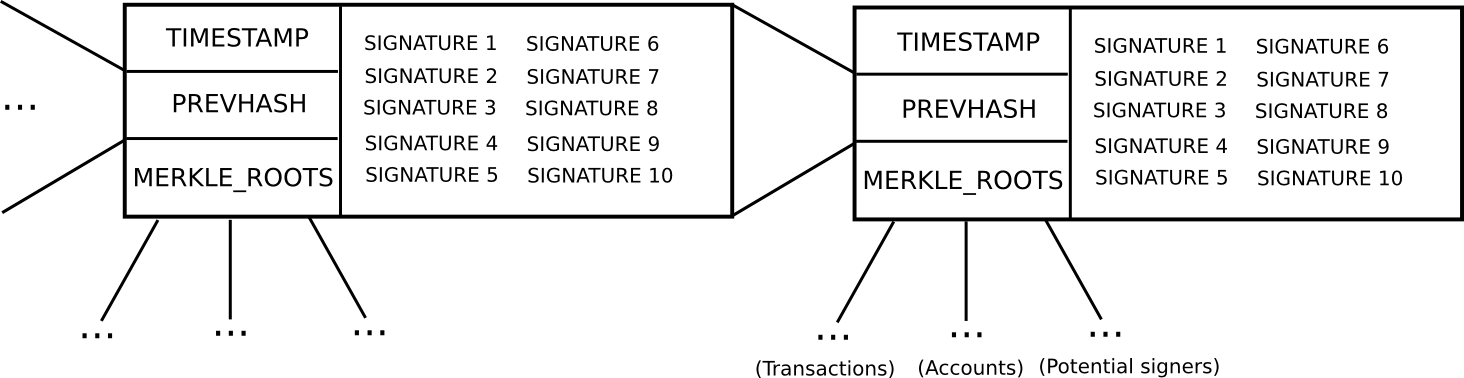
1. So as to be a “potential blockmaker” or “potential signer”, a consumer should put down a safety deposit of some measurement. This safety deposit may be put down at any time, and lasts for an extended time period, say 3 months.
2. Throughout each time slot T (eg. T = 3069120 to 3069135 seconds after genesis), some operate produces a random quantity R (there are lots of nuances behind making the random quantity safe, however they aren’t related right here). Then, suppose that the set of potential signers ps (saved in a separate Merkle tree) has measurement N. We take ps[sha3(R) % N] because the blockmaker, and ps[sha3(R + 1) % N], ps[sha3(R + 2) % N] … ps[sha3(R + 15) % N] because the signers (primarily, utilizing R as entropy to randomly choose a signer and 15 blockmakers)
3. Blocks include a header containing (i) the hash of the earlier block, (ii) the checklist of signatures from the blockmaker and signers, and (iii) the Merkle root of the transactions and state, in addition to (iv) auxiliary information just like the timestamp.
4. A block produced throughout time slot T is legitimate if that block is signed by the blockmaker and at the very least 10 of the 15 signers.
5. If a blockmaker or signer legitimately participates within the blockmaking course of, they get a small signing reward.
6. If a blockmaker or signer indicators a block that isn’t on the primary chain, then that signature may be submitted into the primary chain as “proof” that the blockmaker or signer is making an attempt to take part in an assault, and this results in that blockmaker or signer dropping their deposit. The proof submitter could obtain 33% of the deposit as a reward.

In contrast to proof of labor, the place the motivation to not mine on a fork of the primary chain is the chance price of not getting the reward on the primary chain, in proof of stake the motivation is that in the event you mine on the unsuitable chain you’re going to get explicitly punished for it. That is vital; as a result of a really great amount of punishment may be meted out per dangerous signature, a a lot smaller variety of block headers are required to attain the identical safety margin.

Now, allow us to study what a light-weight shopper must do. Suppose that the sunshine shopper was final on-line N blocks in the past, and desires to authenticate the state of the present block. What does the sunshine shopper have to do? If a light-weight shopper already is aware of {that a} block B[k] is legitimate, and desires to authenticate the following block B[k+1], the steps are roughly as follows:

1. Compute the operate that produces the random worth R throughout block B[k+1] (computable both fixed or logarithmic time relying on implementation)
2. Given R, get the general public keys/addresses of the chosen blockmaker and signer from the blockchain’s state tree (logarithmic time)
3. Confirm the signatures within the block header in opposition to the general public keys (fixed time)

And that is it. Now, there’s one gotcha. The set of potential signers could find yourself altering through the block, so it appears as if a light-weight shopper would possibly have to course of the transactions within the block earlier than having the ability to compute ps[sha3(R + k) % N]. Nonetheless, we are able to resolve this by merely saying that it is the potential signer set from the beginning of the block, or perhaps a block 100 blocks in the past, that we’re deciding on from.

Now, allow us to work out the formal safety assurances that this protocol offers us. Suppose {that a} mild shopper processes a set of blocks, B[1] … B[n], such that each one blocks ranging from B[k + 1] are invalid. Assuming that each one blocks as much as B[k] are legitimate, and that the signer set for block B[i] is decided from block B[i – 100], which means that the sunshine shopper will be capable of appropriately deduce the signature validity for blocks B[k + 1] … B[k + 100]. Therefore, if an attacker comes up with a set of invalid blocks that idiot a light-weight shopper, the sunshine shopper can nonetheless make certain that the attacker will nonetheless should pay ~1100 safety deposits for the primary 100 invalid blocks. For future blocks, the attacker will be capable of get away with signing blocks with faux addresses, however 1100 safety deposits is an assurance sufficient, significantly because the deposits may be variably sized and thus maintain many tens of millions of {dollars} of capital altogether.

Thus, even this older model of Slasher is, by our definition, light-client-friendly; we are able to get the identical sort of safety assurance as proof of labor in logarithmic time.

A Higher Gentle-Consumer Protocol

Nonetheless, we are able to do considerably higher than the naive algorithm above. The important thing perception that lets us go additional is that of splitting the blockchain up into epochs. Right here, allow us to outline a extra superior model of Slasher, that we are going to name “epoch Slasher”. Epoch Slasher is an identical to the above Slasher, apart from a number of different situations:

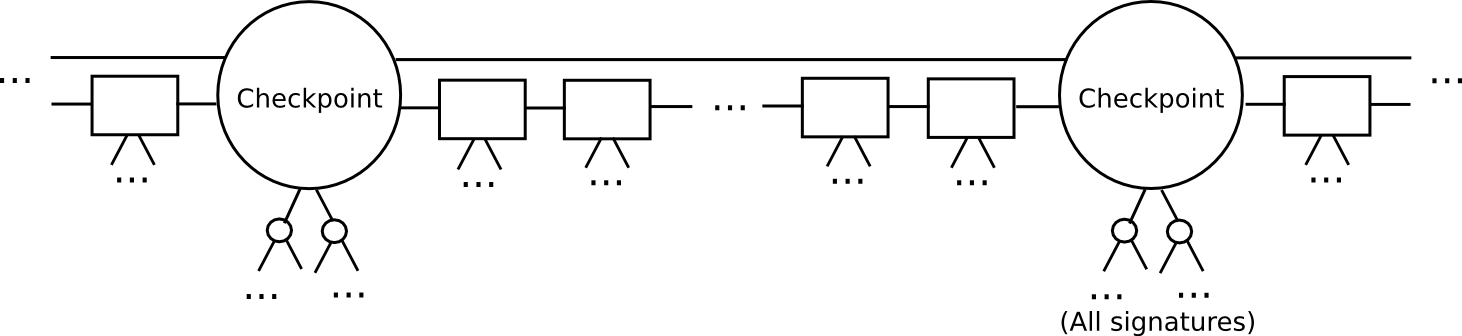
1. Outline a checkpoint as a block such that block.quantity % n == 0 (ie. each n blocks there’s a checkpoint). Consider n as being someplace round a number of weeks lengthy; it solely must be considerably lower than the safety deposit size.
2. For a checkpoint to be legitimate, 2/3 of all potential signers should approve it. Additionally, the checkpoint should instantly embrace the hash of the earlier checkpoint.
3. The set of signers throughout a non-checkpoint block must be decided from the set of signers through the second-last checkpoint.

This protocol permits a light-weight shopper to catch up a lot quicker. As a substitute of processing each block, the sunshine shopper would skip on to the following checkpoint, and validate it. The sunshine shopper may even probabilistically test the signatures, choosing out a random 80 signers and requesting signatures for them particularly. If the signatures are invalid, then we may be statistically sure that 1000’s of safety deposits are going to get destroyed.

After a light-weight shopper has authenticated as much as the newest checkpoint, the sunshine shopper can merely seize the newest block and its 100 mother and father, and use an easier per-block protocol to validate them as within the authentic Slasher; if these blocks find yourself being invalid or on the unsuitable chain, then as a result of the sunshine shopper has already authenticated the newest checkpoint, and by the foundations of the protocol it may be positive that the deposits at that checkpoint are lively till at the very least the following checkpoint, as soon as once more the sunshine shopper can make certain that at the very least 1100 deposits shall be destroyed.

With this latter protocol, we are able to see that not solely is proof of stake simply as able to light-client friendliness as proof of labor, however furthermore it is really much more light-client pleasant. With proof of labor, a light-weight shopper synchronizing with the blockchain should obtain and course of each block header within the chain, a course of that’s significantly costly if the blockchain is quick, as is considered one of our personal design aims. With proof of stake, we are able to merely skip on to the newest block, and validate the final 100 blocks earlier than that to get an assurance that if we’re on the unsuitable chain, at the very least 1100 safety deposits shall be destroyed.

Now, there’s nonetheless a respectable position for proof of labor in proof of stake. In proof of stake, as we have now seen, it takes a logarithmic quantity of effort to probably-validate every particular person block, and so an attacker can nonetheless trigger mild purchasers a logarithmic quantity of annoyance by broadcasting dangerous blocks. Proof of labor alone may be successfully validated in fixed time, and with out fetching any information from the community. Therefore, it might make sense for a proof of stake algorithm to nonetheless require a small quantity of proof of labor on every block, guaranteeing that an attacker should spend some computational effort as a way to even barely inconvenience mild purchasers. Nonetheless, the quantity of computational effort required to compute these proofs of labor will solely must be miniscule.