One of many extra thrilling functions of decentralized computing which have aroused a substantial quantity of curiosity prior to now yr is the idea of an incentivized decentralized on-line file storage system. At the moment, in order for you your information or knowledge securely backed up “within the cloud”, you may have three decisions – (1) add them to your individual servers, (2) use a centralized service like Google Drive or Dropbox or (3) use an current decentralized file system like Freenet. These approaches all have their very own faults; the primary has a excessive setup and upkeep value, the second depends on a single trusted occasion and infrequently includes heavy worth markups, and the third is sluggish and really restricted within the quantity of house that it permits every consumer as a result of it depends on customers to volunteer storage. Incentivized file storage protocols have the potential to supply a fourth approach, offering a a lot increased amount of storage and high quality of service by incentivizing actors to take part with out introducing centralization.
Quite a lot of platforms, together with StorJ, Maidsafe, to some extent Permacoin, and Filecoin, are trying to deal with this drawback, and the issue appears easy within the sense that every one the instruments are both already there or en path to being constructed, and all we’d like is the implementation. Nevertheless, there’s one a part of the issue that’s notably vital: how can we correctly introduce redundancy? Redundancy is essential to safety; particularly in a decentralized community that might be extremely populated by novice and informal customers, we completely can’t depend on any single node to remain on-line. We may merely replicate the info, having just a few nodes every retailer a separate copy, however the query is: can we do higher? Because it seems, we completely can.
Merkle Bushes and Problem-Response Protocols
Earlier than we get into the nitty gritty of redundancy, we are going to first cowl the simpler half: how can we create at the very least a primary system that may incentivize at the very least one occasion to carry onto a file? With out incentivization, the issue is straightforward; you merely add the file, look forward to different customers to obtain it, after which while you want it once more you may make a request querying for the file by hash. If we need to introduce incentivization, the issue turns into considerably tougher – however, within the grand scheme of issues, nonetheless not too laborious.
Within the context of file storage, there are two sorts of actions that you could incentivize. The primary is the precise act of sending the file over to you while you request it. That is simple to do; the most effective technique is a straightforward tit-for-tat recreation the place the sender sends over 32 kilobytes, you ship over 0.0001 cash, the sender sends over one other 32 kilobytes, and many others. Observe that for very giant information with out redundancy this technique is susceptible to extortion assaults – very often, 99.99% of a file is ineffective to you with out the final 0.01%, so the storer has the chance to extort you by asking for a really excessive payout for the final block. The cleverest repair to this drawback is definitely to make the file itself redundant, utilizing a particular sort of encoding to broaden the file by, say, 11.11% in order that any 90% of this prolonged file can be utilized to get better the unique, after which hiding the precise redundancy share from the storer; nevertheless, because it seems we are going to talk about an algorithm similar to this for a special objective later, so for now, merely settle for that this drawback has been solved.
The second act that we will incentivize is the act of holding onto the file and storing it for the long run. This drawback is considerably tougher – how are you going to show that you’re storing a file with out really transferring the entire thing? Thankfully, there’s a resolution that isn’t too troublesome to implement, utilizing what has now hopefully established a well-recognized repute because the cryptoeconomist’s finest pal: Merkle bushes.

Properly, Patricia Merkle could be higher in some circumstances, to be exact. Athough right here the plain outdated unique Merkle will do.
n = 2^okayfor some
okay(the padding step is avoidable, however it makes the algorithm less complicated to code and clarify). Then, we construct the tree. Rename the
nchunks that we obtained
chunk[n]to
chunk[2n-1], after which rebuild chunks
1to
n-1with the next rule:
chunk[i] = sha3([chunk[2*i], chunk[2*i+1]]). This allows you to calculate chunks
n/2to
n-1, then
n/4to
n/2 - 1, and so forth going up the tree till there’s one “root”,
chunk[1].
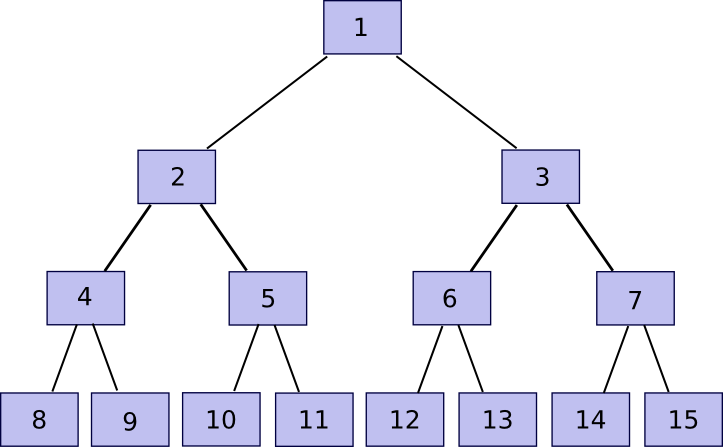
Now, word that should you retailer solely the basis, and overlook about chunk[2] … chunk[2n-1], the entity storing these different chunks can show to you that they’ve any explicit chunk with only some hundred bytes of knowledge. The algorithm is comparatively easy. First, we outline a operate companion(n) which provides n-1 if n is odd, in any other case n+1 – briefly, given a bit discover the chunk that it’s hashed along with in an effort to produce the guardian chunk. Then, if you wish to show possession of chunk[k] with n <= okay <= 2n-1 (ie. any a part of the unique file), submit chunk[partner(k)], chunk[partner(k/2)] (division right here is assumed to spherical down, so eg. 11 / 2 = 5), chunk[partner(k/4)] and so forth right down to chunk[1], alongside the precise chunk[k]. Primarily, we’re offering the whole “department” of the tree going up from that node all the best way to the basis. The verifier will then take chunk[k] and chunk[partner(k)] and use that to rebuild chunk[k/2], use that and chunk[partner(k/2)] to rebuild chunk[k/4] and so forth till the verifier will get to chunk[1], the basis of the tree. If the basis matches, then the proof is okay; in any other case it isn’t.
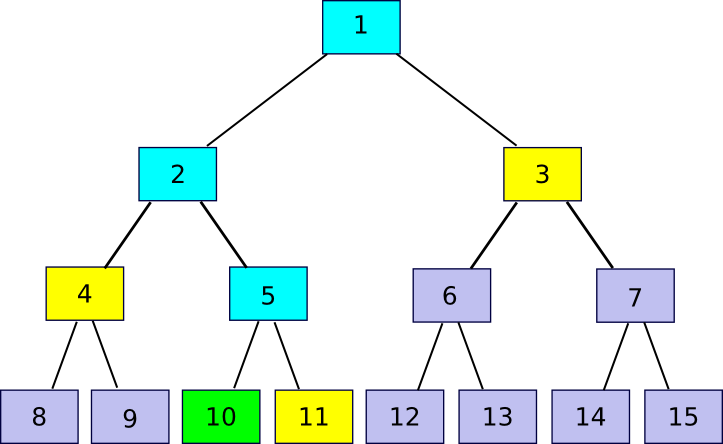
11 = companion(10)), 4 (
4 = companion(10/2)) and three (
3 = companion(10/4)). The verification course of includes beginning off with chunk 10, utilizing every companion chunk in flip to recompute first chunk 5, then chunk 2, then chunk 1, and seeing if chunk 1 matches the worth that the verifier had already saved as the basis of the file.
Observe that the proof implicitly contains the index – typically you’ll want to add the companion chunk on the proper earlier than hashing and typically on the left, and if the index used to confirm the proof is completely different then the proof won’t match. Thus, if I ask for a proof of piece 422, and also you as an alternative present even a sound proof of piece 587, I’ll discover that one thing is incorrect. Additionally, there is no such thing as a approach to supply a proof with out possession of the whole related part of the Merkle tree; should you attempt to go off faux knowledge, in some unspecified time in the future the hashes will mismatch and the ultimate root might be completely different.
Now, let’s go over the protocol. I assemble a Merkle tree out of the file as described above, and add this to some occasion. Then, each 12 hours, I choose a random quantity in [0, 2^k-1] and submit that quantity as a problem. If the storer replies again with a Merkle tree proof, then I confirm the proof and whether it is appropriate ship 0.001 BTC (or ETH, or storjcoin, or no matter different token is used). If I obtain no proof or an invalid proof, then I don’t ship BTC. If the storer shops the whole file, they may succeed 100% of the time, in the event that they retailer 50% of the file they may succeed 50% of the time, and many others. If we need to make it all-or-nothing, then we will merely require the storer to unravel ten consecutive proofs in an effort to get a reward. The storer can nonetheless get away with storing 99%, however then we reap the benefits of the identical redundant coding technique that I discussed above and can describe beneath to make 90% of the file adequate in any case.
One concern that you will have at this level is privateness – should you use a cryptographic protocol to let any node receives a commission for storing your file, would that not imply that your information are unfold across the web in order that anybody can doubtlessly entry them? Thankfully the reply to that is easy: encrypt the file earlier than sending it out. From this level on, we’ll assume that every one knowledge is encrypted, and ignore privateness as a result of the presence of encryption resolves that subject nearly utterly (the “nearly” being that the dimensions of the file, and the occasions at which you entry the file, are nonetheless public).
Seeking to Decentralize
So now we have now a protocol for paying folks to retailer your knowledge; the algorithm may even be made trust-free by placing it into an Ethereum contract, utilizing
block.prevhash as a supply of random knowledge to generate the challenges. Now let’s go to the following step: determining decentralize the storage and add redundancy. The only strategy to decentralize is easy replication: as an alternative of 1 node storing one copy of the file, we will have 5 nodes storing one copy every. Nevertheless, if we merely comply with the naive protocol above, we have now an issue: one node can faux to be 5 nodes and accumulate a 5x return. A fast repair to that is to encrypt the file 5 occasions, utilizing 5 completely different keys; this makes the 5 similar copies indistinguishable from 5 completely different information, so a storer will be unable to note that the 5 information are the identical and retailer them as soon as however declare a 5x reward.
However even right here we have now two issues. First, there is no such thing as a strategy to confirm that the 5 copies of the file are saved by 5 separate customers. If you wish to have your file backed up by a decentralized cloud, you’re paying for the service of decentralization; it makes the protocol have a lot much less utility if all 5 customers are literally storing the whole lot by Google and Amazon. That is really a tough drawback; though encrypting the file 5 occasions and pretending that you’re storing 5 completely different information will stop a single actor from amassing a 5x reward with 1x storage, it can’t stop an actor from amassing a 5x reward with 5x storage, and economies of scale imply even that state of affairs might be fascinating from the perspective of some storers. Second, there’s the problem that you’re taking a big overhead, and particularly taking the false-redundancy subject under consideration you’re actually not getting that a lot redundancy from it – for instance, if a single node has a 50% likelihood of being offline (fairly affordable if we’re speaking a couple of community of information being saved within the spare house on folks’s laborious drives), then you may have a 3.125% likelihood at any level that the file might be inaccessible outright.
There may be one resolution to the primary drawback, though it’s imperfect and it isn’t clear if the advantages are value it. The concept is to make use of a mixture of proof of stake and a protocol referred to as “proof of custody” – proof of simultaneous possession of a file and a non-public key. If you wish to retailer your file, the concept is to randomly choose some variety of stakeholders in some forex, weighting the likelihood of choice by the variety of cash that they’ve. Implementing this in an Ethereum contract may contain having individuals deposit ether within the contract (keep in mind, deposits are trust-free right here if the contract offers a strategy to withdraw) after which giving every account a likelihood proportional to its deposit. These stakeholders will then obtain the chance to retailer the file. Then, as an alternative of the straightforward Merkle tree test described within the earlier part, the proof of custody protocol is used.
The proof of custody protocol has the profit that it’s non-outsourceable – there is no such thing as a strategy to put the file onto a server with out giving the server entry to your personal key on the identical time. Because of this, at the very least in principle, customers might be a lot much less inclined to retailer giant portions of information on centralized “cloud” computing techniques. In fact, the protocol accomplishes this at the price of a lot increased verification overhead, in order that leaves open the query: do we would like the verification overhead of proof of custody, or the storage overhead of getting further redundant copies simply in case?
M of N
No matter whether or not proof of custody is a good suggestion, the following step is to see if we will do some higher with redundancy than the naive replication paradigm. First, let’s analyze how good the naive replication paradigm is. Suppose that every node is offered 50% of the time, and you’re prepared to take 4x overhead. In these circumstances, the prospect of failure is
0.5 ^ 4 = 0.0625 – a quite excessive worth in comparison with the “4 nines” (ie. 99.99% uptime) supplied by centralized providers (some centralized providers provide 5 or 6 nines, however purely due to Talebian black swan concerns any guarantees over three nines can typically be thought-about bunk; as a result of decentralized networks don’t rely upon the existence or actions of any particular firm or hopefully any particular software program package deal, nevertheless, decentralized techniques arguably really can promise one thing like 4 nines legitimately). If we assume that almost all of the community might be quasi-professional miners, then we will scale back the unavailability share to one thing like 10%, through which case we really do get 4 nines, however it’s higher to imagine the extra pessimistic case.
What we thus want is a few sort of M-of-N protocol, very similar to multisig for Bitcoin. So let’s describe our dream protocol first, and fear about whether or not it is possible later. Suppose that we have now a file of 1 GB, and we need to “multisig” it right into a 20-of-60 setup. We break up the file up into 60 chunks, every 50 MB every (ie. 3 GB complete), such that any 20 of these chunks suffice to reconstruct the unique. That is information-theoretically optimum; you may’t reconstruct a gigabyte out of lower than a gigabyte, however reconstructing a gigabyte out of a gigabyte is fully doable. If we have now this sort of protocol, we will use it to separate every file up into 60 items, encrypt the 60 chunks individually to make them appear like unbiased information, and use an incentivized file storage protocol on each individually.
Now, right here comes the enjoyable half: such a protocol really exists. On this subsequent a part of the article, we’re going to describe a chunk of math that’s alternately referred to as both “secret sharing” or “erasure coding” relying on its utility; the algorithm used for each these names is mainly the identical except one implementation element. To start out off, we are going to recall a easy perception: two factors make a line.
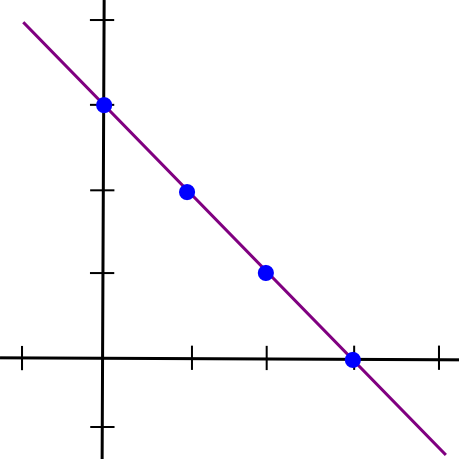
x = 1and the second half because the y coordinate of the road at
x = 2, draw the road, and take factors at
x = 3,
x = 4, and many others. Any two items can then be used to reconstruct the road, and from there derive the y coordinates at
x = 1and
x = 2 to get the file again.
Mathematically, there are two methods of doing this. The primary is a comparatively easy strategy involving a system of linear equations. Suppose that we file we need to break up up is the quantity “1321”. The left half is 13, the proper half is 21, so the road joins (1, 13) and (2, 21). If we need to decide the slope and y-intercept of the road, we will simply clear up the system of linear equations:
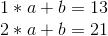
Subtract the primary equation from the second, and also you get:
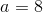
After which plug that into the primary equation, and get:
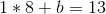
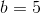
So we have now our equation, y = 8 * x + 5. We are able to now generate new factors: (3, 29), (4, 37), and many others. And from any two of these factors we will get better the unique equation.
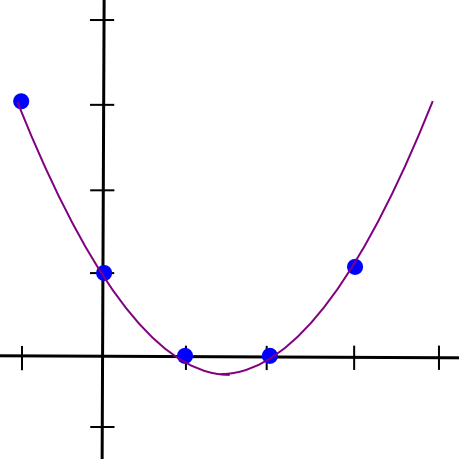
Now, let’s go one step additional, and generalize this into m-of-n. Because it seems, it is extra sophisticated however not too troublesome. We all know that two factors make a line. We additionally know that three factors make a parabola:
x = 1, 2, 3, and take additional factors on the parabola as extra items. If we would like 4-of-n, we use a cubic polynomial as an alternative. Let’s undergo that latter case; we nonetheless maintain our unique file, “1321”, however we’ll break up it up utilizing 4-of-7 as an alternative. Our 4 factors are
(1, 1),
(2, 3),
(3, 2),
(4, 1). So we have now:
Eek! Properly, let’s, uh, begin subtracting. We’ll subtract equation 1 from equation 2, 2 from 3, and three from 4, to cut back 4 equations to 3, after which repeat that course of repeatedly.
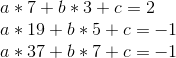
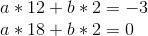
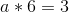
So a = 1/2. Now, we unravel the onion, and get:
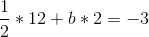
So b = -9/2, after which:
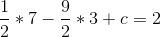
So c = 12, after which:
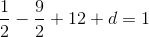
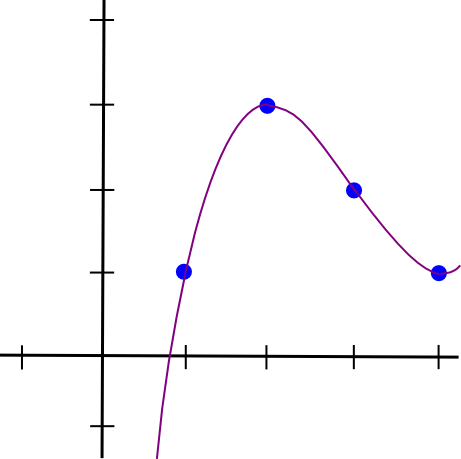
So a = 0.5, b = -4.5, c = 12, d = -7. Here is the stunning polynomial visualized:
I created a Python utility that will help you do that (this utility additionally does different extra superior stuff, however we’ll get into that later); you may obtain it right here. If you happen to wished to unravel the equations shortly, you’ll simply sort in:
> import share > share.sys_solve([[1.0, 1.0, 1.0, 1.0, -1.0], [8.0, 4.0, 2.0, 1.0, -3.0], [27.0, 9.0, 3.0, 1.0, -2.0], [64.0, 16.0, 4.0, 1.0, -1.0]]) [0.5, -4.5, 12.0, -7.0]
Observe that placing the values in as floating level is critical; should you use integers Python’s integer division will screw issues up.
Now, we’ll cowl the simpler strategy to do it, Lagrange interpolation. The concept right here could be very intelligent: we provide you with a cubic polynomial whose worth is 1 at x = 1 and 0 at x = 2, 3, 4, and do the identical for each different x coordinate. Then, we multiply and add the polynomials collectively; for instance, to match (1, 3, 2, 1) we merely take 1x the polynomial that passes by (1, 0, 0, 0), 3x the polynomial by (0, 1, 0, 0), 2x the polynomial by (0, 0, 1, 0) and 1x the polynomial by (0, 0, 0, 1) after which add these polynomials collectively to get the polynomal by (1, 3, 2, 1) (word that I mentioned the polynomial passing by (1, 3, 2, 1); the trick works as a result of 4 factors outline a cubic polynomial uniquely). This won’t appear simpler, as a result of the one approach we have now of becoming polynomials to factors to far is the cumbersome process above, however fortuitously, we even have an specific development for it:
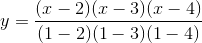
At x = 1, discover that the highest and backside are similar, so the worth is 1. At x = 2, 3, 4, nevertheless, one of many phrases on the highest is zero, so the worth is zero. Multiplying up the polynomials takes quadratic time (ie. ~16 steps for 4 equations), whereas our earlier process took cubic time (ie. ~64 steps for 4 equations), so it is a substantial enchancment particularly as soon as we begin speaking about bigger splits like 20-of-60. The python utility helps this algorithm too:
> import share > share.lagrange_interp([1.0, 3.0, 2.0, 1.0], [1.0, 2.0, 3.0, 4.0]) [-7.0, 12.000000000000002, -4.5, 0.4999999999999999]
The primary argument is the y coordinates, the second is the x coordinates. Observe the other order right here; the code within the python module places the lower-order coefficients of the polynomial first. And at last, let’s get our extra shares:
> share.eval_poly_at([-7.0, 12.0, -4.5, 0.5], 5) 3.0 > share.eval_poly_at([-7.0, 12.0, -4.5, 0.5], 6) 11.0 > share.eval_poly_at([-7.0, 12.0, -4.5, 0.5], 7) 28.0
So right here instantly we will see two issues. First, it seems to be like computerized floating level numbers aren’t infinitely exact in spite of everything; the 12 changed into 12.000000000000002. Second, the chunks begin getting giant as we transfer additional out; at x = 10, it goes as much as 163. That is considerably breaking the promise that the quantity of knowledge you’ll want to get better the file is identical dimension as the unique file; if we lose x = 1, 2, 3, 4 you then want 8 digits to get the unique values again and never 4. These are each critical points, and ones that we’ll resolve with some extra mathematical cleverness later, however we’ll go away them apart for now.
Even with these points remaining, we have now mainly achieved victory, so let’s calculate our spoils. If we use a 20-of-60 break up, and every node is on-line 50% of the time, then we will use combinatorics – particularly, the binomial distribution formulation – to compute the likelihood that our knowledge is okay. First, to set issues up:
> def fac(n): return 1 if n==0 else n * fac(n-1) > def select(n,okay): return fac(n) / fac(okay) / fac(n-k) > def prob(n,okay,p): return select(n,okay) * p ** okay * (1-p) ** (n-k)
The final formulation computes the likelihood that precisely okay servers out of n might be on-line if every particular person server has a likelihood p of being on-line. Now, we’ll do:
> sum([prob(60, k, 0.5) for k in range(0, 20)]) 0.0031088013296633353
99.7% uptime with solely 3x redundancy – step up from the 87.5% uptime that 3x redundancy would have given us had easy replication been the one software in our toolkit. If we crank the redundancy as much as 4x, then we get six nines, and we will cease there as a result of the likelihood both Ethereum or the whole web will crash outright is larger than 0.0001% anyway (actually, you are extra prone to die tomorrow). Oh, and if we assume every machine has 90% uptime (ie. hobbyist “farmers”), then with a 1.5x-redundant 20-of-30 protocol we get a fully overkill twelve nines. Fame techniques can be utilized to maintain monitor of how usually every node is on-line.
Coping with Errors
We’ll spend the remainder of this text discussing three extensions to this scheme. The primary is a priority that you will have ignored studying the above description, however one which is nonetheless vital: what occurs if some node tries to actively cheat? The algorithm above can get better the unique knowledge of a 20-of-60 break up from any 20 items, however what if one of many knowledge suppliers is evil and tries to supply faux knowledge to screw with the algorithm. The assault vector is a quite compelling one:
> share.lagrange_interp([1.0, 3.0, 2.0, 5.0], [1.0, 2.0, 3.0, 4.0]) [-11.0, 19.333333333333336, -8.5, 1.1666666666666665]
Taking the 4 factors of the above polynomial, however altering the final worth to five, offers a very completely different outcome. There are two methods of coping with this drawback. One is the plain approach, and the opposite is the mathematically intelligent approach. The apparent approach is apparent: when splitting a file, maintain the hash of every chunk, and evaluate the chunk in opposition to the hash when receiving it. Chunks that don’t match their hashes are to be discarded.
The intelligent approach is considerably extra intelligent; it includes some spooky not-quite-moon-math referred to as the Berlekamp-Welch algorithm. The concept is that as an alternative of becoming only one polynomial, P, we think about into existence two polynomials, Q and E, such that Q(x) = P(x) * E(x), and attempt to clear up for each Q and E on the identical time. Then, we compute P = Q / E. The concept is that if the equation holds true, then for all x both P(x) = Q(x) / E(x) or E(x) = 0; therefore, apart from computing the unique polynomial we magically isolate what the errors are. I will not go into an instance right here; the Wikipedia article has a superbly first rate one, and you’ll attempt it your self with:
> map(lambda x: share.eval_poly_at([-7.0, 12.0, -4.5, 0.5], x), [1, 2, 3, 4, 5, 6]) [1.0, 3.0, 2.0, 1.0, 3.0, 11.0] > share.berlekamp_welch_attempt([1.0, 3.0, 18018.0, 1.0, 3.0, 11.0], [1, 2, 3, 4, 5, 6], 3) [-7.0, 12.0, -4.5, 0.5] > share.berlekamp_welch_attempt([1.0, 3.0, 2.0, 1.0, 3.0, 0.0], [1, 2, 3, 4, 5, 6], 3) [-7.0, 12.0, -4.5, 0.5]
Now, as I discussed, this mathematical trickery just isn’t actually all that wanted for file storage; the less complicated strategy of storing hashes and discarding any piece that doesn’t match the recorded hash works simply superb. However it’s by the way fairly helpful for one more utility: self-healing Bitcoin addresses. Bitcoin has a base58check encoding algorithm, which can be utilized to detect when a Bitcoin handle has been mistyped and returns an error so you don’t unintentionally ship 1000’s of {dollars} into the abyss. Nevertheless, utilizing what we all know, we will really do higher and make an algorithm which not solely detects mistypes but additionally really corrects the errors on the fly. We do not use any sort of intelligent handle encoding for Ethereum as a result of we desire to encourage use of identify registry-based options, but when an handle encoding scheme was demanded one thing like this may very well be used.
Finite Fields
Now, we get again to the second drawback: as soon as our x coordinates get somewhat increased, the y coordinates begin taking pictures off in a short time towards infinity. To unravel this, what we’re going to do is nothing in need of utterly redefining the principles of arithmetic as we all know them. Particularly, let’s redefine our arithmetic operations as:
a + b := (a + b) % 11 a - b := (a - b) % 11 a * b := (a * b) % 11 a / b := (a * b ** 9) % 11
That “%” signal there’s “modulo”, ie. “take the rest of dividing that vaue by 11”, so we have now
7 + 5 = 1,
6 * 6 = 3(and its corollary
3 / 6 = 6), and many others. We are actually solely allowed to take care of the numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10. The stunning factor is that, at the same time as we do that, all the guidelines about conventional arithmetic nonetheless maintain with our new arithmetic;
(a * b) * c = a * (b * c),
(a + b) * c = (a * c) + (b * c),
a / b * b = aif
b != 0,
(a^2 - b^2) = (a - b)*(a + b), and many others. Thus, we will merely take the algebra behind our polynomial encoding that we used above, and transplant it over into the brand new system. Although the instinct of a polynomial curve is totally borked – we’re now coping with summary mathematical objects and never something resembling precise factors on a airplane – as a result of our new algebra is self-consistent, the formulation nonetheless work, and that is what counts.
> e = share.mkModuloClass(11) > P = share.lagrange_interp(map(e, [1, 3, 2, 1]), map(e, [1, 2, 3, 4])) > P [4, 1, 1, 6] > map(lambda x: share.eval_poly_at(map(e, P), e(x)), vary(1, 9)) [1, 3, 2, 1, 3, 0, 6, 2] > share.berlekamp_welch_attempt(map(e, [1, 9, 9, 1, 3, 0, 6, 2]), map(e, [1, 2, 3, 4, 5, 6, 7, 8]), 3) [4, 1, 1, 6]
The “
map(e, [v1, v2, v3])” is used to transform strange integers into components on this new area; the software program library contains an implementation of our loopy modulo 11 numbers that interfaces with arithmetic operators seamlessly so we will merely swap them in (eg.
print e(6) * e(6)returns
3). You may see that the whole lot nonetheless works – besides that now, as a result of our new definitions of addition, subtraction, multiplication and division all the time return integers in
[0 ... 10] we by no means want to fret about both floating level imprecision or the numbers increasing because the x coordinate will get too excessive.
Now, in actuality these comparatively easy modulo finite fields aren’t what are normally utilized in error-correcting codes; the widely most popular development is one thing referred to as a Galois area (technically, any area with a finite variety of components is a Galois area, however typically the time period is used particularly to consult with polynomial-based fields as we are going to describe right here). The concept is that the weather within the area are actually polynomials, the place the coefficients are themselves values within the area of integers modulo 2 (ie. a + b := (a + b) % 2, and many others). Including and subtracting work as usually, however multiplying is itself modulo a polynomial, particularly x^8 + x^4 + x^3 + x + 1. This quite sophisticated multilayered development lets us have a area with precisely 256 components, so we will conveniently retailer each component in a single byte and each byte as one component. If we need to work on chunks of many bytes at a time, we merely apply the scheme in parallel (ie. if every chunk is 1024 bytes, decide 10 polynomials, one for every byte, lengthen them individually, and mix the values at every x coordinate to get the chunk there).
However it isn’t vital to know the precise workings of this; the salient level is that we will redefine +, –, * and / in such a approach that they’re nonetheless absolutely self-consistent however all the time take and output bytes.
Going Multidimensional: The Self-Therapeutic Dice
Now, we’re utilizing finite fields, and we will take care of errors, however one subject nonetheless stays: what occurs when nodes do go down? At any cut-off date, you may depend on 50% of the nodes storing your file staying on-line, however what you can’t depend on is identical nodes staying on-line perpetually – finally, just a few nodes are going to drop out, then just a few extra, then just a few extra, till finally there aren’t sufficient of the unique nodes left on-line. How can we combat this gradual attrition? One technique is that you could possibly merely watch the contracts which are rewarding every particular person file storage occasion, seeing when some cease paying out rewards, after which re-upload the file. Nevertheless, there’s a drawback: in an effort to re-upload the file, you’ll want to reconstruct the file in its entirety, a doubtlessly troublesome job for the multi-gigabyte motion pictures that are actually wanted to fulfill folks’s seemingly insatiable needs for multi-thousand pixel decision. Moreover, ideally we wish the community to have the ability to heal itself with out requiring energetic involvement from a centralized supply, even the proprietor of the information.
Thankfully, such an algorithm exists, and all we have to accomplish it’s a intelligent extension of the error correcting codes that we described above. The elemental concept that we will depend on is the truth that polynomial error correcting codes are “linear”, a mathematical time period which mainly signifies that it interoperates properly with multiplication and addition. For instance, take into account:
> share.lagrange_interp([1.0, 3.0, 2.0, 1.0], [1.0, 2.0, 3.0, 4.0]) [-7.0, 12.000000000000002, -4.5, 0.4999999999999999] > share.lagrange_interp([10.0, 5.0, 5.0, 10.0], [1.0, 2.0, 3.0, 4.0]) [20.0, -12.5, 2.5, 0.0] > share.lagrange_interp([11.0, 8.0, 7.0, 11.0], [1.0, 2.0, 3.0, 4.0]) [13.0, -0.5, -2.0, 0.5000000000000002] > share.lagrange_interp([22.0, 16.0, 14.0, 22.0], [1.0, 2.0, 3.0, 4.0]) [26.0, -1.0, -4.0, 1.0000000000000004]
See how the enter to the third interpolation is the sum of the inputs to the primary two, and the output finally ends up being the sum of the primary two outputs, after which once we double the enter it additionally doubles the output. So what’s the advantage of this? Properly, here is the intelligent trick. Erasure cording is itself a linear formulation; it depends solely on multiplication and addition. Therefore, we’re going to apply erasure coding to itself. So how are we going to do that? Right here is one doable technique.
First, we take our 4-digit “file” and put it right into a 2×2 grid.
Then, we use the identical polynomial interpolation and extension course of as above to increase the file alongside each the x and y axes:
1 3 5 7 2 1 0 10 3 10 4 8
After which we apply the method once more to get the remaining 4 squares:
1 3 5 7 2 1 0 10 3 10 6 2 4 8 1 5
Observe that it would not matter if we get the final 4 squares by increasing horizontally and vertically; as a result of secret sharing is linear it’s commutative with itself, so that you get the very same reply both approach. Now, suppose we lose a quantity within the center, say, 6. Properly, we will do a restore vertically:
> share.restore([5, 0, None, 1], e) [5, 0, 6, 1]
Or horizontally:
> share.restore([3, 10, None, 2], e) [3, 10, 6, 2]
And tada, we get 6 in each circumstances. That is the stunning factor: the polynomials work equally nicely on each the x or the y axis. Therefore, if we take these 16 items from the grid, and break up them up amongst 16 nodes, and one of many nodes disappears, then nodes alongside both axis can come collectively and reconstruct the info that was held by that exact node and begin claiming the reward for storing that knowledge. Ideally, we will even lengthen this course of past 2 dimensions, producing a three-d dice, a four-dimensional hypercube or extra – the achieve of utilizing extra dimensions is ease of reconstruction, and the associated fee is a decrease diploma of redundancy. Thus, what we have now is an information-theoretic equal of one thing that sounds prefer it got here straight out of science-fiction: a extremely redundant, interlinking, modular self-healing dice, that may shortly domestically detect and repair its personal errors even when giant sections of the dice have been to be broken, co-opted or destroyed.

“The dice can nonetheless operate even when as much as 78% of it have been to be destroyed…”
So, let’s put all of it collectively. You’ve gotten a ten GB file, and also you need to break up it up throughout the community. First, you encrypt the file, and you then break up the file into, to illustrate, 125 chunks. You organize these chunks right into a three-d 5x5x5 dice, determine the polynomial alongside every axis, and “lengthen” each in order that on the finish you may have a 7x7x7 dice. You then search for 343 nodes prepared to retailer every bit of knowledge, and inform every node solely the identification of the opposite nodes which are alongside the identical axis (we need to make an effort to keep away from a single node gathering collectively a whole line, sq. or dice and storing it and calculating any redundant chunks as wanted in real-time, getting the reward for storing all of the chunks of the file with out really offering any redundancy.
In an effort to really retrieve the file, you’ll ship out a request for all the chunks, then see which of the items coming in have the best bandwidth. Chances are you’ll use the pay-per-chunk protocol to pay for the sending of the info; extortion just isn’t a difficulty as a result of you may have such excessive redundancy so nobody has the monopoly energy to disclaim you the file. As quickly because the minimal variety of items arrive, you’ll do the maths to decrypt the items and reconstitute the file domestically. Maybe, if the encoding is per-byte, chances are you’ll even be capable to apply this to a Youtube-like streaming implementation, reconstituting one byte at a time.
In some sense, there’s an unavoidable tradeoff between self-healing and vulnerability to this sort of faux redundancy: if elements of the community can come collectively and get better a lacking piece to supply redundancy, then a malicious giant actor within the community can get better a lacking piece on the fly to supply and cost for faux redundancy. Maybe some scheme involving including one other layer of encryption on every bit, hiding the encryption keys and the addresses of the storers of the person items behind one more erasure code, and incentivizing the revelation course of solely at some explicit occasions may type an optimum stability.
Secret Sharing
At the start of the article, I discussed one other identify for the idea of erasure coding, “secret sharing”. From the identify, it is easy to see how the 2 are associated: if in case you have an algorithm for splitting knowledge up amongst 9 nodes such that 5 of 9 nodes are wanted to get better it however 4 of 9 cannot, then one other apparent use case is to make use of the identical algorithm for storing personal keys – break up up your Bitcoin pockets backup into 9 elements, give one to your mom, one to your boss, one to your lawyer, put three into just a few security deposit packing containers, and many others, and should you overlook your password then you’ll ask every of them individually and chances are high at the very least 5 will provide you with your items again, however the people themselves are sufficiently far other than one another that they are unlikely to collude with one another. This can be a very official factor to do, however there’s one implementation element concerned in doing it proper.
The problem is that this: though 4 of 9 cannot get better the unique key, 4 of 9 can nonetheless come collectively and have numerous details about it – particularly, 4 linear equations over 5 unknowns. This reduces the dimensionality of the selection house by an element of 5, so as an alternative of two256 personal keys to look by they now have solely 251. In case your secret is 180 bits, that goes right down to 236 – trivial work for a fairly highly effective laptop. The best way we repair that is by erasure-coding not simply the personal key, however quite the personal key plus 4x as many bytes of random gook. Extra exactly, let the personal key be the zero-degree coefficient of the polynomial, choose 4 random values for the following 4 coefficients, and take values from that. This makes every bit 5 occasions longer, however with the profit that even 4 of 9 now have the whole selection house of two180 or 2256 to look by.
Conclusion
So there we go, that is an introduction to the ability of erasure coding – arguably the only most underhyped set of algorithms (besides maybe SCIP) in laptop science or cryptography. The concepts right here primarily are to file storage what multisig is to sensible contracts, permitting you to get the completely most doable quantity of safety and redundancy out of no matter ratio of storage overhead you’re prepared to just accept. It is an strategy to file storage availability that strictly supersedes the chances supplied by easy splitting and replication (certainly, replication is definitely precisely what you get should you attempt to apply the algorithm with a 1-of-n technique), and can be utilized to encapsulate and individually deal with the issue of redundancy in the identical approach that encryption encapsulates and individually handles the issue of privateness.
Decentralized file storage continues to be removed from a solved drawback; though a lot of the core know-how, together with erasure coding in Tahoe-LAFS, has already been carried out, there are actually many minor and not-so-minor implementation particulars that also must be solved for such a setup to truly work. An efficient repute system might be required for measuring quality-of-service (eg. a node up 99% of the time is value at the very least 3x greater than a node up 50% of the time). In some methods, incentivized file storage even is dependent upon efficient blockchain scalability; having to implicitly pay for the charges of 343 transactions going to verification contracts each hour just isn’t going to work till transaction charges turn into far decrease than they’re as we speak, and till then some extra coarse-grained compromises are going to be required. However then once more, just about each drawback within the cryptocurrency house nonetheless has a really lengthy strategy to go.

